A Divide and Conquer Sorting Algorithm
O(n log n) - Linearithmic time
What is O(n log n)?
O(n log n) is a Log-linear algorithm with a complexity rank of close to fair, which works by merging two functions, one of which being of 0(n) linear time complexity and the other being of 0(log n) (binary search) time complexity.
EX:
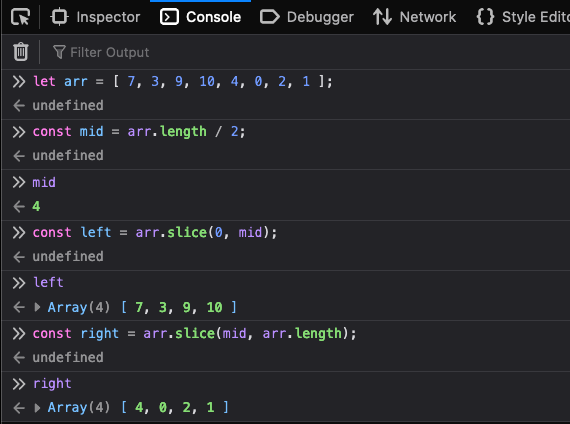
let arr = [ 7, 3, 9, 10, 4, 0, 2, 1 ];
function merge(left,right){ //linear runtime O(n) => based on arr length
let result = [];
while(left.length || right.length) {
if(left.length && right.length) {
if(left[0] < right[0]) {
result.push(left.shift());
} else {
result.push(right.shift());
}
} else if(left.length) {
result.push(left.shift());
} else {
result.push(right.shift());
}
}
return result;
}
// similar to binary search => divides arr into 1/2 on each iteration
// Logarithmic runtime O(log n)
function mergeSort(arr = []){
if(arr.length <= 1){
return arr;
}
// Divide array in 1/2
const mid = arr.length / 2; // create pivot @ index 4 in this case
const left = arr.slice(0, mid); // [ 7, 3, 9, 10 ]
const right = arr.slice(mid, arr.length); // [ 4, 0, 2, 1 ]
// recursively use merge() => ie., calls itself until an exit condition
// is met => based on array.length
return merge(mergeSort(left), mergeSort(right));
}
// 2 functions are merged => Log-linear O(n log n) => o(n) * 0(log n)
// ..better than quadratic O(n^2), but not as good as 0(n) linear,
// O(log n) logarithmic, or O(1) constant
mergeSort(arr); // [ 0, 1, 2, 3, 4, 7, 9, 10 ]
Comments